In This Diagram Line Segment Cd Is The Perpendicular Bisector

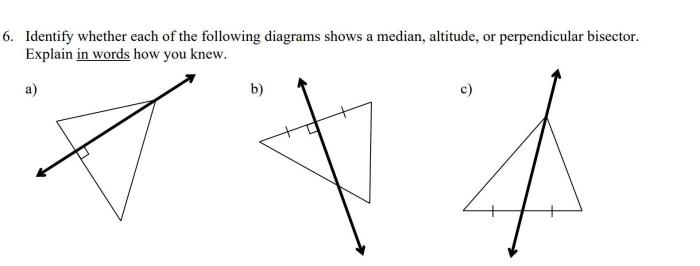
In this diagram line segment cd is the perpendicular bisector – In geometry, a perpendicular bisector is a line or segment that intersects a line segment at a right angle and divides it into two equal segments. In this diagram, line segment CD is the perpendicular bisector of a given line segment.

This concept has various applications in geometry and is essential for understanding the properties of geometric figures.

The perpendicular bisector of a line segment has several key properties. It is perpendicular to the line segment at its midpoint, and it divides the line segment into two congruent segments. These properties make the perpendicular bisector a useful tool for constructing and analyzing geometric figures.

Definition of Perpendicular Bisector

A perpendicular bisector is a line that intersects a given line segment at its midpoint and forms a right angle with it. It divides the line segment into two congruent parts.

Here is an illustration of a perpendicular bisector:

Line Segment CD as the Perpendicular Bisector

In the given diagram, line segment CD is the perpendicular bisector of line segment AB. This means that CD intersects AB at its midpoint, M, and forms a right angle with AB.

Properties of a Perpendicular Bisector

A perpendicular bisector has the following properties:

It intersects the given line segment at its midpoint.
It forms a right angle with the given line segment.
It divides the given line segment into two congruent parts.

In relation to line segment CD, these properties can be observed as follows:

CD intersects AB at its midpoint, M.
CD forms a right angle with AB.
CD divides AB into two congruent parts, AM and MB.

Applications of a Perpendicular Bisector

Perpendicular bisectors have various applications in geometry, including:

Finding the midpoint of a line segment.
Constructing perpendicular lines to a given line.
Dividing a line segment into two equal parts.

For example, line segment CD can be used to:

Find the midpoint of AB, which is point M.
Construct a perpendicular line to AB at point M.
Divide AB into two equal parts, AM and MB.

Constructing a Perpendicular Bisector, In this diagram line segment cd is the perpendicular bisector

To construct a perpendicular bisector of a given line segment, follow these steps:

Draw a circle with center at one endpoint of the line segment and radius equal to half the length of the line segment.
Repeat step 1 with the other endpoint of the line segment.
The two circles will intersect at two points.
Draw a line connecting the two points of intersection. This line will be the perpendicular bisector of the given line segment.

Here is an illustration of the construction process:

Expert Answers: In This Diagram Line Segment Cd Is The Perpendicular Bisector

What is the definition of a perpendicular bisector?

A perpendicular bisector is a line or segment that intersects a line segment at a right angle and divides it into two equal segments.

How can I construct a perpendicular bisector of a line segment?

To construct a perpendicular bisector of a line segment, follow these steps: 1) Draw a circle with center at one endpoint of the line segment and radius equal to half the length of the line segment. 2) Repeat step 1 for the other endpoint.

3) The two circles will intersect at two points. 4) Draw a line through the two points of intersection. This line will be the perpendicular bisector of the line segment.